L-Systems in Architecture (2003)
This project dates back to 2003. A link to the original Flash presentation is at the bottom of this page.
A Brief Introduction to L-Systems
A Lindenmayer System is a formal grammar that was initially conceived of as a theory of plant growth. L-Systems can model complex forms of plants using relatively few simple rules.
L-Systems consist of two parts: a generative and an interpretative process. The main concept of the generative process is string-rewriting, in which letters that comprise and initial string are replaced in parallel by new letters according to pre-defined rules. Together, these new letters form a new generation of string, which can then be subjected to the same replacement rules. This string rewriting process is usually repeated for several iterations.
In the second part of the L-System, the letters of the final generation of string are interpreted. This project explores the visual interpretation of string as geometric forms. It primarily uses the concept of turtle graphics, borrowed from the Logo programming language, to translate individual letters into drawing commands.
In the first part of the system, a string is generated by successively rewriting an initial string according to specific replacement rules. The system has three distinct inputs: an initial string, one or more replacement rules, and a number of times to perform the rewriting operation.
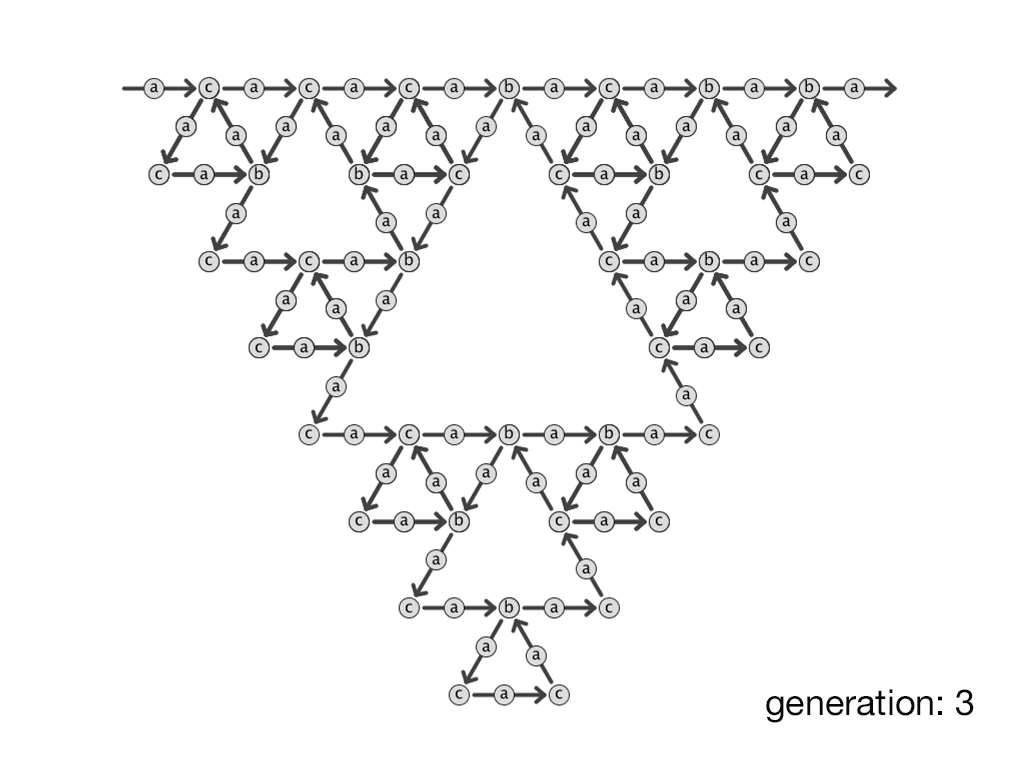
In the following example, the intial string a is rewritten three times to create abacabaabacabaacaba.
Inputs:
• Initial string: a
• Replacement rules:
1) a aba
2) b ac
• Iterations: 3
Replacement Process:
0) a
1) aba
2) abaacaba
3) abacabaabacabaacaba
In the second part of the system, letters of the generated string are interpreted. This project mostly uses turtle graphics to turn the string into a geometric form.
In turtle graphics, a fictive turtle follows movement commands that correspond to individual letters of a string. The turtle's path is thus a visual interpretation of the string. A two-dimensional turtle graphics system could consist of three letters that correspond to the following commands:
a : move turtle forward
b : turn turtle right 60°
c : turn turtle left 60°
The animated example uses these three commands, together with the following inputs, to create a from that resembles a Serpinski triangle:
• Initial string: a
• Replacement rules: a abacacaba
• Iterations: 0, 1, 2, 3, 4
Expanding the L-Systems Logic
The L-Systems algorithm described above can be expanded to facilitate the production of architectural geometries. In a first step, turtle graphics commands are ammended to control movement in 3D space. In such an environment, voluminous geometries can then be generated through extrusion along the turtle's path, or by using path segments to create surfaces (e.g. lofting).
To allow a single L-Sytem to create many permutations of a design, stochastic replacement rules can be formulated. In addition, replacement rules can be limited in the their scope to only apply to certain generations of the rewriting process.
Further geometric freedom is obtained by introducing variable parameters directly into the turtle graphics language. Finally, the system is expanded to incorporate environmental interaction, so that the turtle executes different strings depending on the local conditions it encounters.
In lieu of fixed replacement rules, one can introduce stochastic rules so that a letter is replaced by a fist string with a specific probability, and otherwise replaced by another string. Indeed, any number of replacement scenarios are conceivable. In the example below, the following rules are applied:
• Replacement rules:
1) d d[cad]a (p=50%)
2) d d[bad]a (p=50%)
• Iterations: 3
a : move forward (draw line)
b : turn right
c : turn left
[ : save position
] : revert to last saved position
The resulting system produces an irregular branching structure caused by the random numbers in the replacement process. By allowing these random numbers to also fluctuate each time the system is run, many different permutations of a design can be produced.
In order to control the L-Systems drawing rules with a higher degree of precision, it is useful to introduce parameters into the string rewriting rules. On a most basic level, this can include specification of incremental changes for to the turtle's state. For example:
X(=45) : set incremental x-axis rotation to 45°
L(=1.2) : set forward distance to 1.2 units
This syntax can be further expanded to include mathematical functions, conditionality, as well as independent variables:
X(=sin(M*90)) : set x-axis rotation to depend on sine value of x-position (M)
L(=1,2) : set forward distance to random number between 1 and 2 units
X(=if(Y>90,45,60)) : set value of X conditionally, depending on value of Y
The L-Systems logic is particularly well suited to the production of modular systems. As not every letter of string needs to correspond to a turtle instruction, one can introduce letters that are simply replaced by groups of other letters. For example, in a system in which a implies move forward and c implies turn right, a new letter d could be defined to create a square:
d acacaca
A square, signified by letter d, can now be used as part of other modules, which in turn can become components of yet larger modules. Thus the L-Systems logic can be used not only to create a spatial organization of components, but for the differentiation and articulation of these components.
By introducing parameters into the component definitions - as described in the section above - the components become flexibile and adaptable to local conditions.
Towards Responsiveness
L-Systems can be a powerful design tool. Minimal inputs can create a spatially complex output. The string-rewriting logic is particularly suitable to forms that contain branching, recursion, and modularity. By expanding the logic to include independent parameters, one can not only gain a high degree of control over the produced form, but can potentially become adaptive.
Thus the constructive parameters of the form can be linked to the turtle's spatial position, orientation, and even to proximity to already produced components. A system that at first glance may appear overly deterministic thereby becomes highly responsive.
Does such an L-Systems process still model nature? Or should we try to explore the specific nature of these man-made processes?
All objects in this project are generated using a custom Excel program with VisualBasic macros. The Excel program creates the L-Systems string according to the specified replacment rules. It then interprets this string and produces a construction script (MEL) for the Maya CAD program to visualize the form.
This approach uses Excel's intuitive interface, while leveraging Maya's geometric routines (lofting, extruding, visualizing, etc). An optional specific time-code for each drawing instruction allows Maya to animate the sequential interpretation of the string.
The screenshots show three stages of the Excel program: 1) specification of the replacement rules, 2) generation of L-Systems string, 3) interpretation of the string as a construction script for Maya.
Launch the complete 2003 L-Systems presentation:
L-Systems in Architecture (requires Flash)Further background: The Algorithmic Beauty of Plants (PDF), by Przemysław Prusinkiewicz